1. Stacks and queues-SPL

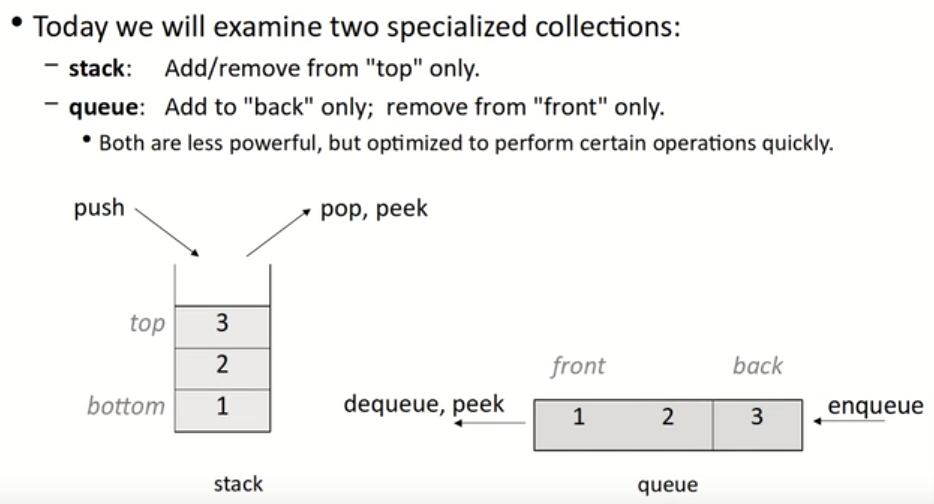
今天我们将学习两个用于特定功能的集合（collections）：

• 栈（stack）：仅从“top”位置添加/删除元素。
• 队列（queue）：仅从“end”位置添加元素，仅从“front”位置删除元素。
• 这两个集合虽然功能较少，但是针对特定操作进行了快速执行的优化。

2. Stacks

2.1 Concepts

栈：基于添加元素和以相反顺序检索它们的原则的集合。

• 后进先出（”LIFO”）
• 元素按插入顺序存储。我们不认为它们具有索引。
• 客户端只能添加/删除/检查最后添加的元素（即”顶部”）。

基本栈操作：

• push：将元素添加到顶部。
• pop：删除顶部元素。
• peek：查看顶部元素。

既然Vector拥有stack的所有功能，那我们为什么还需要stack呢，因为stack是一种用于某些专门用途的数据结构。

并且stack本身也比vector更加轻量，使用的内存更少，并且核心操作函数（peek()、pop()、push()）的时间复杂度都是O(1)，因此当用于某些特定用途时，stack明显更为合适。

2.2 Stacks in computer science

编程语言和编译器：

• 函数调用会被放置在一个栈上（调用=入栈，返回=出栈）
• 编译器使用栈来计算表达式

匹配相关的成对事物：

• 判断一个字符串是否为回文串
• 检查一个文件，查看其花括号 { } 是否匹配
• 将“中缀”表达式转换为前缀或后缀形式

复杂算法：

• 使用backtracking在迷宫中进行搜索
• 许多程序使用undo stack保存之前的操作记录

2.3 Stack-SPL

下图是SPL中的stack的大部分方法，当然我们也可以把stack打印到cout或者output stream中：

同样是介绍在SPL中使用的方法：

#include "stack.h" // SPL

stack<int> s;     // {0}    bottom -> top
s.push(42);       // {42}
s.push(-3);       // {42，-3}
s.push(17);       // {42，-3，17}

cout << s.pop() << endl;   // 17   (s is {42,-3})
cout << s.peek() << endl;  // -3   (s is {42,-3})
cout << s.pop() << endl;   // -3   (s is {42})

此外，如果你想在stack中像其他语言一样可以存储超类型object元素,yeah,但你为此必须得使用pointer(指针),我们会在接下来的几周里学到pointer；如果你想创建一个stack of objects,你可以像在其他语言中直接创建一个stack of objects,这意味着会复制每个object元素；你也可以创建一个stack of pointers,让pointer元素指向object对象所在的地址,这样就可以避免object对象的复制。

2.4 Stack limitations/idioms

不能用索引（S[i]）的方式访问一个stack。每次只能从stack中弹出一个元素。

我们通常用while(!s.empty()){}的方式去遍历一个栈，每次访问一个元素，都会导致这个元素被删除（因为只有用s.pop()函数才能访问到下面的元素），所以如果不希望元素被删除，那么就不用stack。

2.5 Stack implementation

Stack内部一般是用Array或者Vector实现的。

• bottom = index 0
• top = index (size - 1)

当然stack也可以用linked list实现。

• top = front node

当Stack用Vector实现时，它的Insert操作的平均时间复杂度是O(1)：在它需要扩容之前，都是O(1)是显而易见的；当进行第n+1次时，就需要扩容，显然这次操作是O(n)，但是如果与前面的所有操作进行复杂度均摊，那么会发现每一次操作平均要2次移动，所以平均下来仍然是常数阶的时间复杂度，即O(1)。

3. Queues

队列：按照添加顺序检索元素。

• 先进先出（“FIFO”）
• 元素按照插入的顺序存储，但没有索引。
• 只能在队列的末尾添加元素，只能检查/删除队列的前端元素。

基本队列操作：

• 入队（enqueue）：将一个元素添加到队列的末尾。
• 出队（dequeue）：移除队列的第一个元素。
• 查看（peek）：查看队列的第一个元素但不将其移除。

3.1 Queues in computer science

操作系统：

• 打印作业队列，用于发送到打印机的作业
• 程序/进程队列，用于运行待执行的程序/进程
• 网络数据包队列，用于发送数据包

编程：

• 模拟客户或顾客排队的队列
• 存储按顺序执行的计算的队列

现实世界的例子：

• 乘客在自动扶梯上或排队等候
• 在加油站（或生产线）等待的汽车

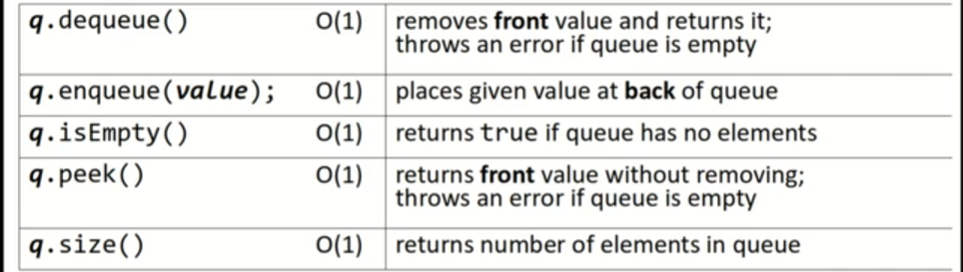
3.2 The Queue class-SPL

同样是介绍SPL库中的queue：

#include "queue.h" // SPL

Queue<int> q;  // {}  front -> back
q.enqueue(42); // {42}
q.enqueue(-3); // {42，-3}
q.enqueue(17); // {42，-3，17}
cout << q.dequeue() << endl; // 42 ( q is {-3，17})
cout << q.peek() << endl;    // -3 ( q is {-3，17})
cout << q.dequeue() << endl; // -3 ( q is {17})

3.3 Queues idioms(常用遍历方式)

像stack一样，必须把元素从queue中取出来后才能访问他们：

// process ( and destroy ) an entire queue
while (!q.isEmpty()) {
	do something with q.dequeue();
}

// 这种方法可以在最后保持queue原来样子的基础上遍历queue
// 即运行完q.dequeue()后，马上再运行一次q.enqueue()
// 这样运行完后queue还是原来的样子
// 但是不能直接去获取size的值，在程序开始前获取一次，使用到结束即可
int size = q.size();
for (int i = 0; i < size; i++) {
    do something with q.dequeue();
    (including possibly re-adding it to the queue)
}

3.4 Mixing stacks and queues

我们经常为了达成某种效果而把stacks和queues混在一起使用，如：逆序queue中的元素。

#include "stack.h" // SPL
#include "queue.h" // SPL

Queue<int> q;
q.enqueue(1);
q.enqueue(2);
q.enqueue(3); // {1,2,3}

Stack<int> s;

while (!q.isEmpty()) {   // transfer queue to stack
	s.push(q.dequeue()); // q={}  s={1,2,3}
}

while (!s.isEmpty()) {
    q.enqueue(s.pop());  // q={3,2,1}  s={}
}
cout << q << endl;       // {3,2,1}

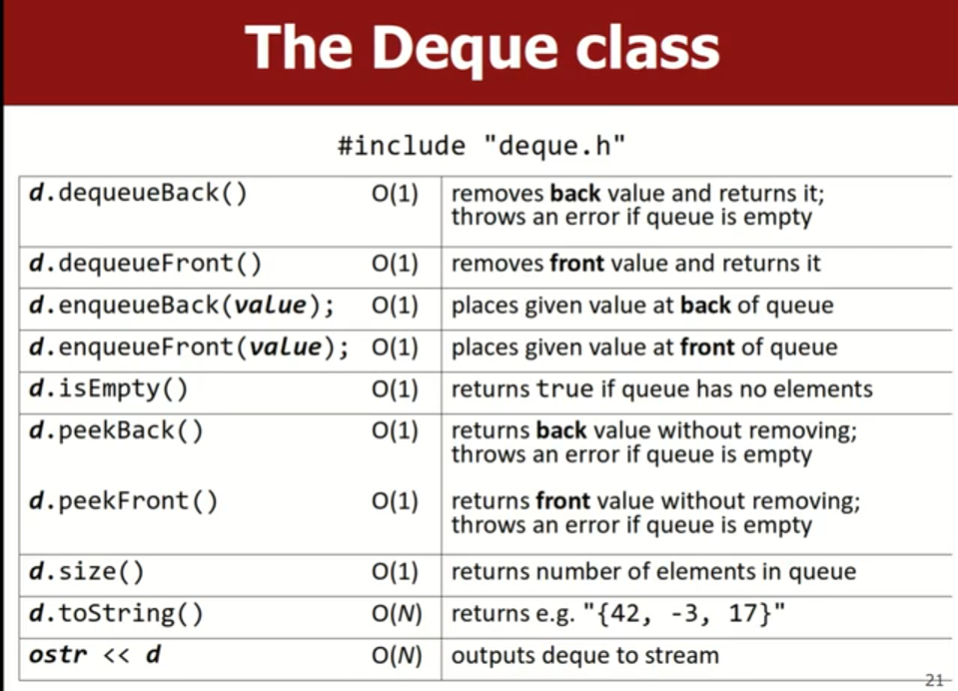
3.5 deques(双向的queue)

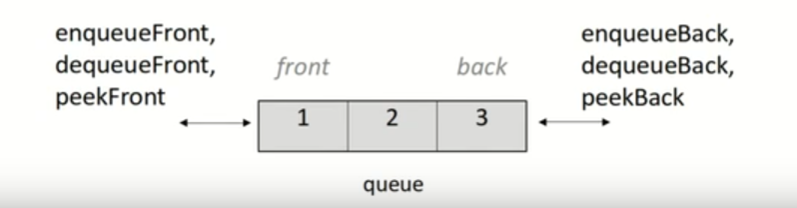
双向queue，头部和尾部都可以进行enqueue或dequeue的操作。结合了stack和queue的功能，很少用。但是在SPL中仍然定义了它：#include "deque.h"。

双端队列（deque）：一种双端开口的队列。

• 可以从任一端添加/删除元素。
• 组合了栈和队列的许多优点。
• 通常使用linked list实现。

基本双端队列操作：

• 在前端/后端添加元素（enqueueFront/Back）；
• 在前端/后端删除元素（dequeueFront/Back）；
• 查看前端/后端元素（peekFront/Back）。