1. Collections：Vector

1.1 Vector概要

我们介绍的Vector依然是Stanford的SPL的项目库。c++的vector在java与JavaScript中被称为array，在Python中被称为list。例如我们之前说的Grid、Java中的array，它的大小一经指定后就是是不变的，除非我们调用函数主动地去修改它；而python中的list的大小可以随程序的运行而动态的增加或减小其容量大小，此外，Java中的ArrayList也可以随程序运行而动态改变其容量大小。

// vector: a collection of elems with 0-based indexes.
// like a dynamically-resizing array (Java's ArrayList or Python's list)
#include "vector.h" // SPL

// initialize a vector containing 5 integers
Vector<int> nums{42, 17, -6, 0, 28};

Vector<string> names;
names.add("stu");  // 尾插法依次插入记录
names.add("Marty");
names.insert(0,"ed"); // 指定索引位置插入一条记录

1.2 Why not arrays？

C++中的Array与Vector的作用是有些类似的，大部分场景都可以互换，但是我们基本上不用Array，我们总是会选择用Vector，Array真的很糟糕，原因如下：

  1. Array一经声明后大小就是固定的，很难去改变其大小，我们甚至很难知道它实际的大小（元素的个数），因为Array对象本身没有length field。
  2. 当我们越界访问Array时，会访问到垃圾内容，甚至报错，C++对这些没有检测与提示机制，只会在出现相关问题时直接报错。
  3. Array对象基本上没有什么成员函数方法，如insert、delete、倒序、元素排序，元素查找等等。

1.3 Vector members

image-20230624211457564

根据注释和function名称很容易知道每个函数的作用是什么。注意ostr << v，STL的vector类没有这样的直接输出的功能。

1.4 Iterating over a vector

#include "vector.h" // SPL
#include <string.h>
#include <iostream>
using namespace std;

Vector<string> names {"Ed", "Hal","sue"};

// 下面列举出几种遍历vector的方式
for (int i = 0; i < names.size(); i++) {
    cout << names[i] << endl;    // for loop
}

// 如果过程中需要进行插入/删除操作，最好用这种方式
for (int i = names.size() - 1; i >= 0; i--) {
	cout << names[i] << endl;    // for loop, backward
}

for (string name : names) {
    cout << name << endl;       // "for-each" loop
}

for (string &name : names) {
    name += "!";              // "for-each" loop by reference
}

注意，C++有一个规则，当我们把对象a的值传递给对象b时，如果我们不使用引用传递，那么程序会复制一份对象a的拷贝给对象b。

1.5 Insert/Delete

此外，当我们使用for-each loop遍历vector时，最好不要进行insert/delete操作，这会改变vector的结构，可能我们看到的值就不是原来应该看到的值，甚至会有内存错误等等。但是`for loop`操作可以在遍历的过程中进行insert或remove操作，但是最好使用`for loop backward`的方式。举例如下：

// 如果过程中需要进行插入/删除操作，最好用for loop backward.
for (int i = names.size() - 1; i >= 0; i--) {
	if (names[i] == string("cxk")) {
		names.remove(i);
	}
}

// for loop的方式会导致连续出现的目标元素被遗漏
for (int i = 0; i < names.size(); i++) {
	if (names[i] == string("cxk")) {
		names.remove(i);
	}
}

// 不要在for each loop中做元素的增删
for (string name : names) {
	names.insert(3,"cxzc");
	names.remove(3);
    cout << name << endl;       // "for-each" loop
}

上面提到，当进行remove操作时，若采用for loop的方式，当目标元素连续出现时（index上紧邻），那么就会遗漏掉起码一个元素；因为本质上来说，在vector中，我删除了一个元素并执行i++，就相当于一次性向右移动了两个元素的距离，因此连续出现的目标元素就会有至少一个被遗漏，因为后面的元素我们还没有访问过。

Remove()操作完delete_pos右侧元素整体向左移动一个单位，之后i指针向右一个单位(i++)，这就相当于指针i一次性向右移动了两个单位。

若采用for loop backward则不会有这种问题，因为后面的元素我们都访问过了，无所谓向后移几格，只是会有重复访问的情况出现，但是这种方式得到的结果是绝对正确的。当然我们可以在for loop的方式上加一些修正，这样也可以让它的执行过程变正确，但是如果追求代码的简洁性，那么for loop backward是最优解。

当我们执行Insert/Remove操作时，离index0越近，花费的时间就越长，因为我们要移动更多的元素。

1.6 Nested Vectors

即在vector中的元素也是vector，从它的样子上来看，它更像一个二维数组，即Grid，但与Grid相比，它的每一行的长度可以是不同的；而Grid的每一行长度必须是相同的，表现出来要是一个矩形。

#include "vector.h"  // SPL

Vector<int> row1 {1};
Vector<int> row2 {2, 3};
Vector<int> row3 {4, 5, 6};
Vector<Vector<int> > vv; // "> >"之间隔了一个空格，原因是可有可无的

vv.add(row1);
vv.add(row2);
vv.add(row3);
// { {1}, {2, 3}, {4, 5, 6} }
cout << vv << endl;       
cout << vv[1][1] << endl; // 3

// quicker initialization
Vector<Vector<int> > vv { {1}, {2, 3}, {4, 5, 6} };

注意这些功能只在SPL中有，STL中不一定会有这些内容。此外，还有上面的”> >”中间隔了一个空格，其实没啥关系，加不加都无所谓，不影响结果的正确。

但是在旧的C++编译器中，这可能会有问题，如果不加空格，旧版本的c++编译器会认为这是一个与stream相关的read符号，使编译器产生误解。为了兼容8年前的c++编译器，这一步操作确实很有必要。

此外，我们未来可能会用到grid of vectors或vector of map，或别的复合型的collection，因此事先学习这些是有必要的。

1.7 Vector Implementation

image-20230625151028126

当我们谈到array时，指代的总是一段负责存储数据的固定大小的内存空间。

一个vector有三个成员：array，size，capacity。一般来说size总是小于capacity的，这样方便随时增加新的元素。我们在vector中不断地加入元素，直到size >= capacity时，当前array的元素就会被复制到一个新的更大的array中（此时发生的事情是capacity变大，因此需要一块新的更大的内存空间）。

3.Big-Oh Notation

关于程序运行效率的内容，用Big-Oh标记法来量化程序运行的效率。

3.1 Efficiency（效率）

Efficiency：代码使用计算资源的度量，可以是运行速度（运行时间），也可以是内存使用量（空间度量），以及还有很多种别的资源等等。大多数情况下Efficiency指的是运行时间（runtime）。

为了更好度量程序运行效率，做出如下的假设，这是简化后的模型：

image-20230626095301400

规定一条语句的运行时间设为1个时间单位（这里不考虑语句的差异，如乘法运算的时间要比加法运算更长）。、因此，基于简化后的时间效率模型，当我们看到一段代码，要计算它的时间效率时，只需要弄清楚这段代码从开始到结束所要执行的语句的次数即可（注意这里是次数，因为有的语句在loop中，因此会执行多次）。

3.2 Algorithm growth rates

image-20230626102246250

即对于上述分析出来的一个运行语句结果，我们认为它的时间效率可以被认为是O（N^3^），即我们只关注影响该程序时间的最显著的项，这意味着，当N的值开始增大时，我们的时间消耗是以N^3^ 的增长率开始增长的。

如第一个add操作的时间效率是O(1)。这并不意味着我们把一个元素放到vector的末尾真的只需要一个时间单位，O(1)只是意味着在执行该操作的时候，所花费的时间与vector中元素的数量无关。

大O标记法代表在我们加大输入的数据量时，算法执行时间的增长率。还有平均运行时间效率，即把最好和最坏的情况相加/2，就是average-case runtime。本质上就是我们常说的时间复杂度。

3.3 时间复杂度的常见类型

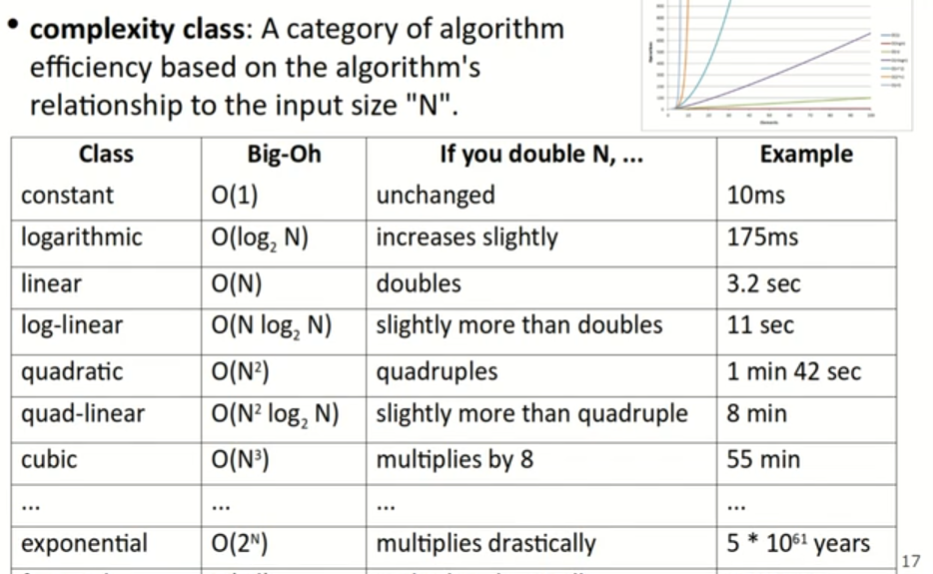
image-20230717141503620

上面是一系列的常见的算法时间复杂度，N是输入数据的大小，可以看到对于不同的时间复杂度，当我们把数据规模N加倍后，算法运行所花费的时间的增长情况也是有很大的不同的，所以尽量选择时间复杂度较低的算法。