Recursive Backtracking1

回溯法：通过尝试部分解决方案来找到整个解决方案，如果期间有不合适的部分，那么马上丢弃他们。与上节课的穷尽搜索不同的是，回溯法会像穷举搜索一样去搜索所有可能的空间，但是回溯不会保留所有可能的结果，它会在搜索过程中进行筛选，过滤掉不合适的方案。

回溯：撤销本次决策，回到上一次决策的位置，重新进行决策。如走迷宫。

diceRolls：每次选择做完后，都需要完成自我清理，使状态回溯到之前的状态，准备找下一种情况。当然可以通过使用值传递的方式避免每次自我清理，但是每次调用都会造成大量的复制操作，浪费资源。

Core1：reduce search space

缩小搜索空间是回溯法的核心所在，我们可以提前预判哪些分支是不必要执行的，提前将其过滤掉。

DiceSum1是用来小试身手，练习了进一步缩小空间的操作；DiceSum2则进一步提出了更高的要求，要求我们输出的结果中每个结果的排列必须是唯一的，不可出现以乱序排列的形式出现的重复结果是不被接受的。这个只需要让序列严格按照从小到大的顺序去遍历，这样就不会有相同组合的结果以不同顺序反复出现的现象了。

子集问题

同样可以用backtracking思想解决，但是这里就不再变成每个decision有几个choices了，而是每个decision都只有两个choices：是否包含当前正在处理的元素。这样就形成了一个二叉树。

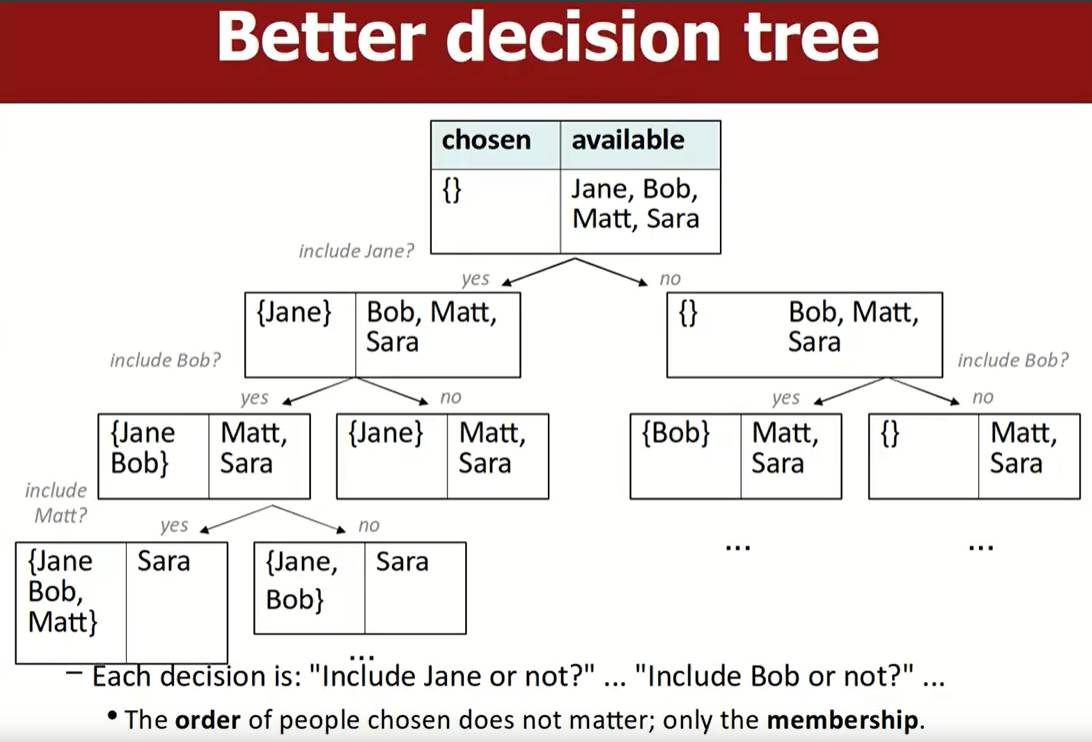
backtracking在执行的过程中是从左向右的，即先把最左侧分支执行完毕，因此我们在每做完一次选择后，需要将当前参与决策的element再放回去，否则右侧的分支就没有这个结果可以选择了，比如说做左侧的对Matt的决策，我们取出Matt后，做完这步决策后，需要将Matt再放回去，因为右侧的所有决策树都需要Matt这个元素。

Backtracking2

n queens problem（n皇后问题）

八皇后问题是一个以国际象棋为背景的问题：如何能够在8×8的国际象棋棋盘上放置八个皇后，使得任何一个皇后都无法直接吃掉其他的皇后？为了达到此目的，任两个皇后都不能处于同一条横行、纵行或斜线上。八皇后问题可以推广为更一般的n皇后摆放问题：这时棋盘的大小变为n×n，而皇后个数也变成n。当且仅当n = 1或n ≥ 4时问题有解[1]。

Decision：每次决定应该是决定往下一列放置皇后。Choice：每次决定中的选择是该往当前列中的哪里放置皇后。

每当发现当前放置choice不安全时，就回退（Undo-choice）。这种方法适合找出所有的放置方案。

提前停止backtracking

如果我们只想从n皇后问题中找到一种解法，那么需要一种机制，当我们发现已经有一个解决方案时，可以告诉整个递归程序让他优雅的终止。

思考：如果要求要打印的result的数量，当达到这个数量时，再退出；那么该如何进行操作？

Travel问题

写一个函数travel，travel函数接受一个坐标(x,y)，该函数需要打印出所有可能到达该坐标的路径，只允许在东、南、东南三个方向移动，每次只允许移动一步。这也就意味着我们不能回头。

思路

同样，按照backtracking的思路，base-case是当前位置已经到达了目标位置，而recursive case是依次尝试向三个方向前进，并在每一次尝试后退回，以尝试下一个方向。